Механические колебания

При первом подвешивании груз будет колебаться с частотой \[\nu_1=\dfrac{1}{2\pi}\sqrt{\dfrac{k_1}{m}}\] \(k_1\) - жесткость пружины.
Во втором случае жесткость пружины изменится, а именно удвоится, так как при параллельном подвешивании жесткости суммируются и будет равна \(k_2=2k_1\). А груз будет колебаться с частотой \[\nu_2=\dfrac{1}{2\pi}\sqrt{\dfrac{k_2}{M}}\] По условию \(\nu_2=2\nu_1\), значит \[\dfrac{1}{2\pi}\sqrt{\dfrac{k_2}{M}}=2\dfrac{1}{2\pi}\sqrt{\dfrac{k_1}{m}}\Rightarrow \sqrt{\dfrac{2k_1}{M}}=2\sqrt{\dfrac{k_1}{m}}\] Возведем обе части в квадрат \[\dfrac{2k_1}{M}=\dfrac{4k_1}{m}\Rightarrow M=\dfrac{m}{2}=1\text{ кг}\]

Ответ: 1

Запишем второй закон Ньютона для шарика на вертикальную и горизонтальную оси \[\begin{cases} T' \sin \alpha=ma\\ T'\cos \alpha -mg=0\\ \end{cases}\] где \(m\) – масса груза, \(T'\) – сила натяжения нити, \(a\) –центростремительное ускорение. Также \(a=\dfrac{v^2}{R}\) \(R\) – радиус окружности вращения, а \(R=l\sin \alpha \). Значит второй закон ньютона выглядит следующим образом \[\begin{cases} T' \sin \alpha=\dfrac{mv^2}{l\sin \alpha } \\ T'\cos \alpha -mg=0\\ \end{cases}\] Из второго уравнения выразим силу натяжения нити и подставим в первое \[\begin{cases} T'=\dfrac{mg}{\cos \alpha}\\ \dfrac{mg\sin \alpha}{\cos \alpha}=\dfrac{mv^2}{l\sin \alpha }\\ \end{cases}\] отсюда скорость движения шарика равна \[v=\sqrt{\dfrac{gl\sin^2\alpha}{\cos \alpha }}\] Период обращения находится по формуле: \[T=\dfrac{2 \pi R}{v}=\dfrac{2\pi l \sin \alpha}{v}=2 \pi \sqrt{\dfrac{ l^2\sin^2 \alpha \cos \alpha }{gl \sin^2 \alpha }}=2 \pi \sqrt{\dfrac{l \cos \alpha }{g}}=2 \cdot 3,14 \sqrt{\dfrac{0,15 \text{ м}\cdot0,5 }{10\text{ м/с$^2$}}} \approx 0,54\text { с}\]

Ответ: 0,54

Запишем второй закон Ньютона для шарика на вертикальную и горизонтальную оси \[\begin{cases} T' \sin \alpha=ma\\ T'\cos \alpha -mg=0\\ \end{cases}\] где \(m\) – масса груза, \(T'\) – сила натяжения нити, \(a\) –центростремительное ускорение. Также \(a=\dfrac{v^2}{R}\) \(R\) – радиус окружности вращения, а \(R=l\sin \alpha \). Значит, второй закон ньютона выглядит следующим образом \[\begin{cases} T' \sin \alpha=\dfrac{mv^2}{l\sin \alpha } \\ T'\cos \alpha -mg=0\\ \end{cases}\] Из второго уравнения выразим силу натяжения нити и подставим в первое \[\begin{cases} T'=\dfrac{mg}{\cos \alpha}\\ \dfrac{mg\sin \alpha}{\cos \alpha}=\dfrac{mv^2}{l\sin \alpha }\\ \end{cases}\] Угловая скорость равна \[\omega= v l\sin \alpha\] Значит второе уравнение из системы можно переписать в виде \[\dfrac{g}{\cos \alpha}=\omega^2 l \sin \alpha \Rightarrow l=\dfrac{g}{\omega^2\cos \alpha}=\dfrac{10\text{ м/с$^2$}}{25\text{ рад$^2$/с$^2$ \cdot 0,5}}=0,8\text{ м}\]

Ответ: 0,8

Запишем закон сохранения импульса при столкновении бруска и тела \[mv=v'(M+m) \Rightarrow mv=4mv' \Rightarrow v'=\dfrac{v}{4} \quad (1)\] где \(v'\) – скорость бруска и тела после столкновения.
Чтобы вернуться в точку удара бруску надо пройти расстояние \(2L\) и совершить половину колебания на пружине. Период колебаний пружинного маятника равен \[T=2 \pi \sqrt{\dfrac{M+m}{k}}=2\pi \sqrt{\dfrac{4m}{k}} \quad (2)\] Значит время, затрачивоемое на возвращение тела обратно, равно \[t=\dfrac{2L}{v'}+\dfrac{T}{2}\] С учетом (1) и (2) оно равно \[t=\dfrac{8L}{v}+\pi \sqrt{\dfrac{4m}{k}}\] Отсюда начальная скорость бруска \[v=\dfrac{8L}{t-\pi \sqrt{\dfrac{m}{k}}}=\dfrac{8\cdot 0,25\text{ м}}{1,7-3,14\sqrt{\dfrac{0,1\text{ кг}}{40\text{ Н/м}}}}\approx 1,3 \text{ м/с}\]

Ответ: 1,3

Запишем закон сохранения импульс в момент удара и закон сохранения энергии после удара и до подъема на максимальную высоту \[\begin{cases} mv_0=(m+M)v_1 \\ \dfrac{(m+M)v_1^2}{2}=\dfrac{(m+M)v_2^2}{2}+(m+M)g 2l\\ \end{cases}\] где \(v_1\) – скорость пули и шарика после удара, \(v_2\) – скорость в наивысшей точке, \(M\) – масса шарика.
Кроме того, максимальность груза означает, что в наивысшей точке сила натяжения нити обращается в ноль (но только в наивысшей). Для второго закона Ньютона это выглядит следующим образом \[(m+M)g=(m+M)a \Rightarrow (m+M)g= \dfrac{(m+M)v_2^2}{l} \Rightarrow v_2^2=gl\] Подставим \(v_2\) в закон сохранения энергии и выразим \(v_1\) \[v_1=\sqrt{gl+4gl}=\sqrt{5gl}\] Из закона сохранения импульса найдем массу шарика \[M=m \left(\dfrac{v_0}{\sqrt{5gl}}-1 \right)=0,01\text{ кг}\left(\dfrac{300\text{ м/с}}{\sqrt{5\cdot 10\text{ Н/кг}\cdot 0,5\text{ м}}}-1 \right)=59\text{ г}\]

Ответ: 59

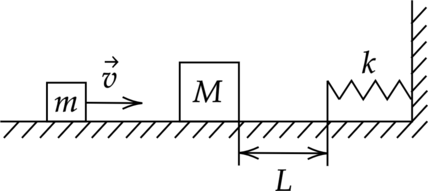
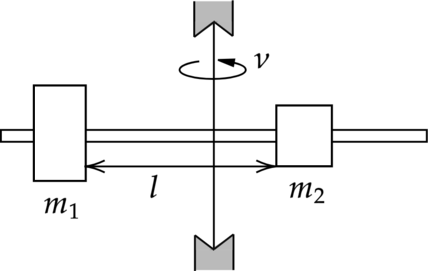
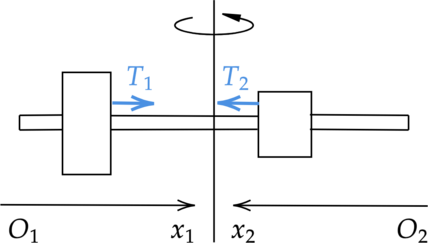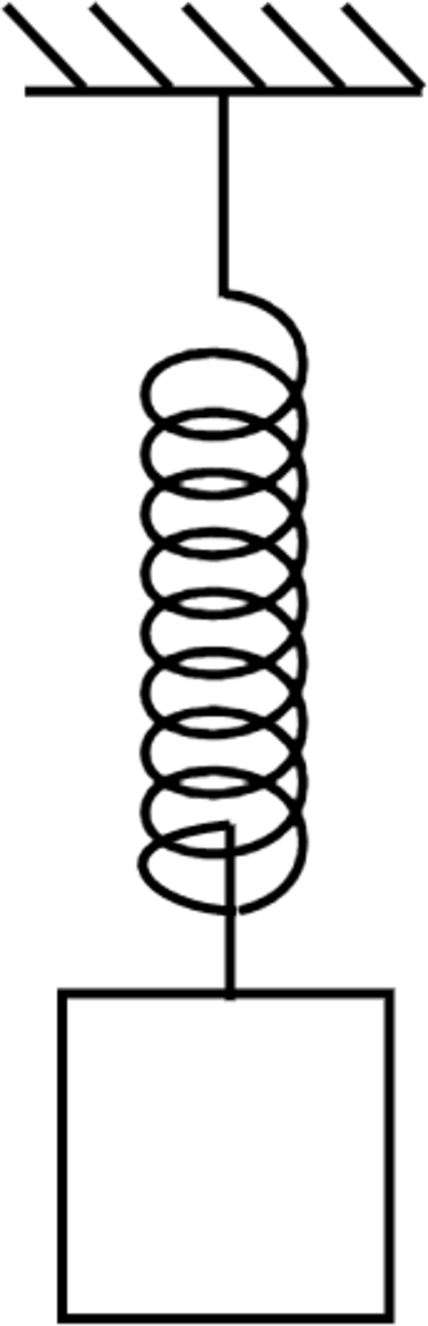
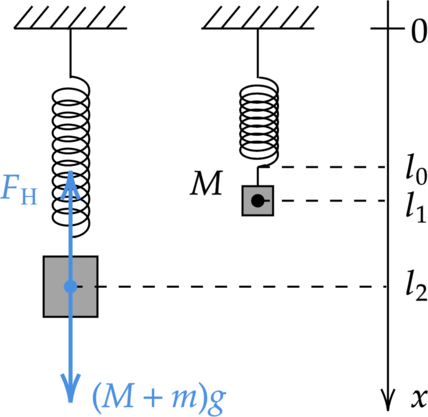Для каждого груза выберем инерциальную систему отсчёта, ось которой направлена вдоль штанги к оси вращения (см. рисунок), и запишем в проекциях второй закон Ньютона для грузов: \[\begin{cases} T_1= m_1 a_1\\ T_2=-m_2a_2\\ \end{cases}\] где \(a_1=\omega ^2R_1\), \(a_2=\omega^2R_2\) – центростремительные ускорения грузов, \(\omega=2\pi \nu\) – циклическая частота, \(R\) – радиус обращения.
Так как \(T_1=T_1\), а \(R_1+R_2=l\), то найдем радиус обращения первого груза из системы уравнений и силу натяжения нити. \[R_1=\dfrac{m_2}{m_1+m_2}l, \hspace{10 mm} T=\dfrac{m_1m_2}{m_1+m_2}(2\pi \nu)^2 l\] Отсюда частота обращения \[\nu=\dfrac{1}{2\pi}\sqrt{\dfrac{T(m_1+m_2)}{m_1m_2l}}=\dfrac{1}{2 \cdot 3,14}\sqrt{\dfrac{95\text{ Н}(0,1\text{ кг}+ 0,4\text{ кг})}{0,1\text{ кг}\cdot 0,4\text{ кг}\cdot 0,3\text{ м}}}\approx 10\text{ об/с}\]

Ответ: 10

В начальном положении тело находилось в равновесии, то есть сила тяжести уравновешивает силу Гука \[(m+M)g=k(l_2-l_0) \quad(1)\] После отделения части груза, будут совершаться гармонические колебания, значит по закону сохранения энергии \[\dfrac{k(l_2-l_0)^2}{2}=\dfrac{k(l_1-l_0)^2}{2}+Mg(l_2-l_1) \quad (2)\] где \(М\) — масса оставшейся части груза, \(l_0\) — длина пружины в нерастянутом состоянии, \(l_2\) — длина пружины в исходном состоянии, \(l_1\) — длина пружины в состоянии максимального подъёма оставшейся части груза.
Также \(l_2-l_1=h \quad (3) \) и \(l_1-l_0=(l_2-l_0)-h \quad (4)\) C учетом (1), (2), (3) и (4) получим, что масса отделившейся части груза равна \[m=\dfrac{hk}{2g}=\dfrac{0,03\text{ м}\cdot 400\text{ Н/м}}{2\cdot 10\text{ Н/кг}}=0,6\text{ кг}\]

Ответ: 0,6