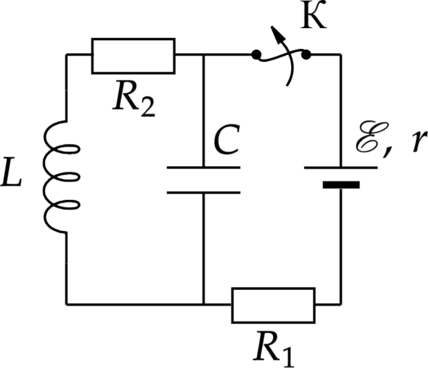
В электрическую цепь подключены источника тока с ЭДС и внутренним сопротивлением \(\xi=100\) В и \(r=5\) Ом соответственно, два резистора \(R_1=10\) Ом и \(R_2=15\) Ом, конденсатор ёмкостью \(C=50\) мкФ и катушка индуктивности \(L\) (см. рисунок). После размыкания ключа на резисторе \(R_2\) выделяется количество теплоты равное \(W=100\) мДж. Найдите индуктивность катушки \(L\). Сопротивлением провода катушки пренебречь. Ответ дайте в мГн.
Пока ключ замкнут в цепи будет устанавливаться сила тока \[I=\dfrac{\xi}{R_1+R_2+r}, \quad (1)\] При этом напряжение на конденсаторе равно напряжению на резисторе \(R_2\), то есть \[U=\dfrac{\xi R_2}{R_1+R_2+r} \quad (2)\] На резисторе \(R_2\) будет выделятся энергия конденсатора и энергия катушки, потому что при размыкании ключа резистор \(R_1\) не будет включен в цепь и ток через него не пойдет \[W=\dfrac{LI^2}{2}+\dfrac{CU^2}{2}, \quad (3)\] Объединяя (1), (2) и (3), получим \[W=\dfrac{L\xi^2}{2(R_1+R_2+r)^2}+\dfrac{C \xi^2R_2^2}{2(R_1+R_2+r)^2}\] Отсюда индуктивность катушки \[L=\dfrac{\left(2W(R_1+R_2+r)^2- C\xi^2R_2^2\right)}{\xi^2}\] \[L=\dfrac{2\cdot 100\text{ мДж}(5\text{ Ом}+10\text{ Ом}+15\text{ Ом})^2-50\text{ мкФ}\cdot 10^4\text{ В$^2$}\cdot 225\text{ В$^2$}}{10^4\text{ В$^2$}}=6,75\text{ мГн}\]
Ответ: 6,75



