Законы сохранения в механике (страница 2)

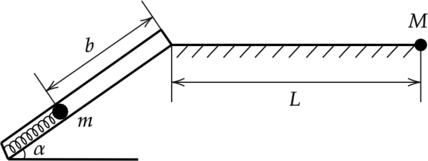
В процессе движения по дулу будет справедлив закон сохранения энергии \[E_n=E_k+E_{n1},\] где \(E_n\) – потенциальная энергия сжатой пружины, \(E_k\) – кинетическая энергия шарика при вылете из желоба, а \(E_{n1}\) – потенциальная энергия шарика при вылете из желоба. Расписав энергии по формулам получим: \[E_n=\dfrac{mv^2}{2}+ mgb\sin{\alpha} \quad (1)\] Движение шайбы после вылета из дула рассмотрим с точки зрения кинематики. Движение по оси, направленной вдоль поверхности земли будет равномерное, а движения по оси, перпендикулярной поверхности, будет равнозамедленное, с ускорение \(g\). Напишем уравнение координаты в точке \(M\). Пусть ось Ох направлена вдоль поверхности, ось Оу направлена перпендикулярно поверхности движения. \[\begin{cases} Ox: L=vt \cos{\alpha} \\ Oy: 0=vt\sin{\alpha}-\dfrac{gt^2}{2}\\ \end{cases}\] где \(v\) – скорость шарика при вылете из дула, \(t\) – время полета шарика. Выразим из второго уравнения время и подставим его в первое. \[t=\dfrac{2v\sin{\alpha}}{g}\] \[L=\dfrac{2v^2 \sin{\alpha}\cos{\alpha}}{g}\] Выразим из последнего уравнения \(v^2\) \[v^2=\dfrac{Lg}{\sin{2\alpha}}\quad (2)\] Подставим (2) в (1) и получим \[E_n=\dfrac{mgL}{2\sin{2\alpha}+mgb\sin{\alpha}}=mg\left(\dfrac{L}{2\sin{\alpha}}+b\sin{\alpha}\right)=0,1\text{ кг}\cdot 10\text{ Н/кг}\left({\dfrac{1\text{ м}}{2\cdot 1}+0,5\text{ м}\dfrac{\sqrt{2}}{2}}\right)\approx 0,85\text{ Дж}\]

Ответ: 0,85

Запишем систему уравнений, состоящую из закона сохранения импульса и закона сохранения энергии \[\begin{cases} E_k=E_{k1}+A_{\text{тр.}}\\ p_\text{пл}-p_\text{бр}=p\\ \end{cases}\] где \(E_k\) – кинетическая энергия пластилина и бруска после столкновения, \(E_{k1}\) – кинетическая энергия бруска и пластилина после уменьшения скорости в 2 раза, \(p\) – импульс системы после столкновения, \(p_\text{бр}\) и \(p_\text{пл}\) – импульс бруска и пластилина соответственно. Расписав по формулам, получим \[\begin{cases} \dfrac{(m+4m)v^2}{2}=\dfrac{(m+4m)v_1^2}{2} + \mu(m+4m)gS\quad (1)\\ mv_\text{пл}4m_\text{бр}=(m+4m)v\\ \end{cases}\] где \(v\) – скорость после столкновения, \(v_1\) – скорость, при уменьшении в два раза \(v_1=\dfrac{v}{2}\), \(S\) – искомое расстояние
Из второго уравнения найдем скорость после столкновения \[5v=v_\text{пл}4v_\text{бр} \Rightarrow v=\dfrac{v_\text{пл}-4v_\text{бр}}{5}=\dfrac{25\text{ м/с}-4\cdot 5\text{ м/с}}{5}=1\text{ м/с}\] Так как \(v_1=\dfrac{v}{2}\), то \(v_1=0,5\) м/с Подставим в (1) найденные скорости и выразим расстояние \[S=\dfrac{v^2-v_1^2}{2\mu g}=\dfrac{1\text{ м/с}-0,25\text{ м/с}}{2\cdot0,1875\cdot 10\text{ м/с$^2$}}=0,2\text{ м}\]

Ответ: 0,2

Запишем второй закон Ньютона в момент, когда шарик касается бруска \[F_\text{тяж}-T=ma_\text{цс},\] где \(F_\text{тяж}\) – сила тяжести, \(a_\text{цс}\) – центростремительное ускорение.
Распишем все составляющие закона по формулам и получим: \[T-mg=m\dfrac{v^2}{l}\] \(v\) – скорость перед столкновением с бруском. Выразим скорость перед столкновением \[v=\sqrt{\dfrac{l(T-mg)}{m}} \quad (1)\] Также запишем закон сохранения импульса при абсолютно неупругом ударе \[p_1+p_2=p_0\] где \(p_1\) – импульс шарика, \(p_2\) – импульс бруска, \(p_0\) – импульс бруска и шарика после удара. Распишем все составляющие по формулам, с учетом того, что брусок покоится \[mv=(m+M)v_0\] Выразим массу бруска \[M=\dfrac{mv-mv_0}{v_0} \quad (2)\] Подставим (1) в (2) \[M=\dfrac{m\left(\sqrt{\dfrac{l(T-mg)}{m}}-v_0\right)}{v_0}=\dfrac{0,5\text{ кг}\left(\sqrt{\dfrac{1\text{ м}( 8,6\text{ Н}-0,5\text{ кг}\cdot 10\text{ Н/кг})}{0,5\text{ кг}}}-0,4\text{ м/с}\right)}{0,4\text{ м/с}}=2,5\text{ кг}\]

Ответ: 2,5

Запишем второй закон Ньютона в момент, когда шарик оторвется от поверхности сферы, это означает, что сила реакции опоры будет равна нулю, и ускорение будет создаваться только силой тяжести \[(m+99m)g\cos \alpha =\dfrac{(m+99m)v^2}{R}\] С учетом того, что \(\cos \alpha=\dfrac{h}{R}\) имеем \[\dfrac{g h}{R}=\dfrac{v^2}{R} \Rightarrow v=\sqrt{gh} \quad (1)\] Запишем закон сохранения импульса в момент, когда пуля касается бруска \[mv_0=(m+99m)u\] Отсюда скорость после столкновения \[u=\dfrac{mv_0}{100m}\quad (2)\] Также запишем закон сохранения энергии \[E_{k1}+E_{n1}=E_{k2}+E_{n2},\] где \(E_{k1}\) – кинетическая энергия после столкновения(на высоте \(R\)), \(E_{n1}\) – потенциальная энергия тела на высоте \(R\), \(E_{k2}\) – кинетическая энергия на высоте \(h\), \(E_{n2}\) – потенциальная энергия на высоте \(h\). Расписав все слагаемые по формулам получим \[\dfrac{(m+99m)u^2}{2}+(m+99m)gR=\dfrac{(m+99m)v^2}{2}+(m+99m)gh \quad (3)\] Подставим (1), (2) в (3) \[\dfrac{m^2v^2_0}{2(100m)^2}+gR=\dfrac{gh}{2}+gh\] Отсюда радиус полусферы \[R=\dfrac{3h}{2}-\dfrac{m^2v^2_0}{2g(100m)^2}=\dfrac{3\cdot 1,4\text{ м}}{2}-\dfrac{0,0001\text{ кг}\cdot40000\text{ м$^2$/с$^2$}}{2\cdot 10\text{ м/с$^2$}\cdot 1\text{ кг}}=1,9\text{ м}\]

Ответ: 1,9

При падении шарика его потенциальная энергия на высоте \(H\) преобразуется в кинетическую энергию на высоте \(h\) и потенциальную на высоте \(h\) \[mgH=\dfrac{mv^2}{2}+mgh\] где \(m\) – масса шарика, \(v\) – его скорость на высоте \(h\).
Выразим скорость \[v=\sqrt{2g(H-h)} \quad (1)\] При отскоке его скорость по вертикали преобразуется в скорость по вертикали и горизонтали, по вертикали она станет равна \[v_y=v \sin \beta\] При это на максимальной высоте скорость равна 0, значит приращение высоты составит \[\Delta h =\dfrac{0-v^2 \sin^2 \beta }{-2g}\] Значит, высота подъема равна \[h_1=h+\Delta h= h+ \dfrac{v^2 \sin^2 \beta }{2g}=h+ \dfrac{v^2 \sin ^2(90-2 \alpha)}{2g}\] с учетом (1) имеем \[h_1=h+(H-h)\cos ^2 2\alpha =2 \text{ м}+(3 \text{ м}-2\text{ м})\dfrac{1}{4}=2,25\text{ м}\]

Ответ: 2,25

I способ
Запишем второй закон Ньютона на ось, совпадающую с движением тела. \[Mg\sin \alpha= Ma \Rightarrow a= g\sin \alpha\] Тело будет двигаться по наклонной поверхности с ускорением \(g\sin \alpha\). У нас имеется формула расстояния \[x=\dfrac{u^2-v_0^2}{2a}\] где \(u\) и \(v_0\) – конечная и начальная скорости тела, \(a\) – ускорение тела.
В нашем случае тело двигается из состояния покоя, то есть \[x=\dfrac{u^2}{2g\sin \alpha}\] Отсюда конечная скорость равна \[u=\sqrt{2gx \sin \alpha }\quad (1)\] Воспользуемся законом сохранения импульса \[mv-Mu=(m+M)V\] где \(V\) – скорость составного тела сразу после попадания пули.
Отсюда \(V\) \[V=\dfrac{mv-Mu}{m+M}\] или же с учетом (1) \[V=\dfrac{mv-M\sqrt{2gx\sin \alpha }}{m+M}\quad (2)\] Дальше воспользуемся первоначальным уравнением расстояния, с учетом того, что ускорение \(-g\sin \alpha\), а конечная скорость равна 0 \[S=\dfrac{-V^2}{-2g\sin \alpha}\] или с учетом (2) \[S=\dfrac{\left(mv-M\sqrt{2gx\sin \alpha }\right) ^2}{(m+M)^2 2g\sin \alpha}\] II способ Запишем закон сохранения энергии при движении бруска вниз по наклонной плоскости \[mgx\sin \alpha =\dfrac{mu^2}{2} \Rightarrow u=\sqrt{2gx\sin \alpha } \quad (1)\] где \(u\) – конечная скорость тела.
Воспользуемся законом сохранения импульса \[mv-Mu=(m+M)V\] где \(V\) – скорость составного тела сразу после попадания пули.
Отсюда \(V\) \[V=\dfrac{mv-Mu}{m+M}\] или же с учетом (1) \[V=\dfrac{mv-M\sqrt{2gx\sin \alpha }}{m+M}\quad (2)\] Запишем закон сохранения энергии при движении тела вверх по наклонной плоскости \[\dfrac{(M+m)V^2}{2}=(M+m)Sg\sin \alpha\] Тогда с учетом (2) \(S\) равно \[S=\dfrac{\left(mv-M\sqrt{2gx\sin \alpha }\right) ^2}{(m+M)^2 2g\sin \alpha}=\dfrac{\left(0,005\text{ кг}\cdot 500\text{ м/с}-0,3\text{ кг}\sqrt{2\cdot 10\text{ м/с$^2$}\cdot 3,6\text{ м}0,5 }\right) ^2}{(0,005\text{ кг}+0,3\text{ кг})^2 2\cdot 10\text{ м/с$^2$} \cdot 0,5}\approx 0,53 \text{ м}\]

Ответ: 0,53

Запишем систему уравнений, состоящую из закона сохранения импульса и закона сохранения энергии \[\begin{cases} E_n+E_k=E_{k1}\\ p_0=p_1\\ \end{cases}\] где \(E_n\) – потенциальная энергия мяча на высоте \(H\), \(E_k\) – кинетическая энергия шара на высоте \(H\), \(E_{k1}\) – кинетическая энергия шара при столкновении с землей, \(p\) – импульс до столкновения с землей, \(p_1\) – импульс после столкновения с землей. Расписав по формулам, получим \[\begin{cases} mgH+\dfrac{mv^2}{2}=\dfrac{mv_1^2}{2}\quad (1)\\ 0,5mv_1=mv_2\\ \end{cases}\] где \(m\) – масса шарика, \(v\) – начальная скорость, \(v_1\) – скорость перед столкновением с землей, \(v_2\) – скорость после столкновения с землей. Из второго уравнения скорость после столкновения равна \(v_2=0,5v_1\).
Запишем закон сохранения энергии при движении вверх до высоты \(h\) \[\dfrac{mv_2^2}{2}=mgh\] Выразим скорость \[v_2=\sqrt{2gh} \quad (2)\] Значит \[v_1=\dfrac{\sqrt{2gh}}{0,5} \quad (3)\] Подставим (2) и (3) в (1) и выразим начальную скорость. \[v=\sqrt{2\left(\dfrac{2gh}{0,5^2}-gH\right)}=\sqrt{2g\left(\dfrac{2h}{0,25}-H\right)}=\sqrt{2\cdot 10\text{ м/с$^2$}\left(\dfrac{2\cdot 3\text{ м}}{0,25}-4\text{ м}\right)}\approx 13\text{ м/с}\]

Ответ: 13