Векторы в физике

Закрепленный вектор — упорядоченная пара точек (направленный отрезок, имеющий начало и конец).

Обозначать можем следующими способами: \(\overrightarrow{AB}\), где \(A\) — начало, а \(B\) — конец вектора или просто \(\vec{a}\).

Длина вектора — расстояние между началом и концом вектора.

Длина векторов обозначается следующим образом: \(|\vec{a}|\) или \(|\overrightarrow{AB}|\).

Если задана прямоугольная система координат, и координаты начала и конца вектора заданы в ней парами \(A=(x_1,y_1)\) и \(B=(x_2,y_2)\) соответственно, тогда координаты вектора можно задать \[\overrightarrow{AB}=\{\,x_2-x_1, y_2-y_1\,\}\]

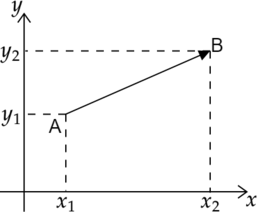
Тогда длина вектора \(\overrightarrow{AB}\) задается формулой

\[|\overrightarrow{AB}|=\sqrt{(x_2-x_1)^2-(y_2-y_1)^2}\]

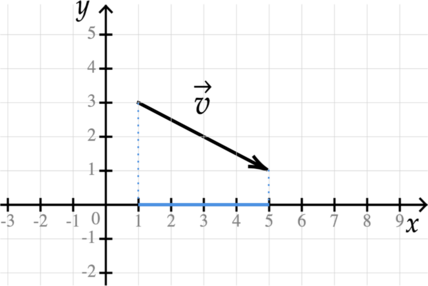
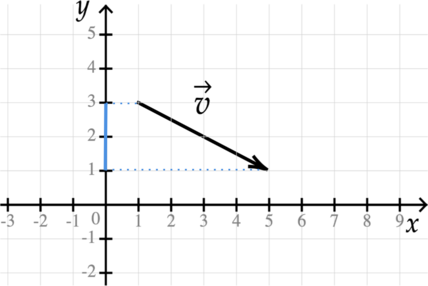
Проекцией вектора на какую-либо ось называется длина отрезка между проекциями начала и конца вектора на эту ось, взятая со знаком <<\(\displaystyle +\)>> или <<\(\displaystyle -\)>>.

Например, проекцией вектора \(\overrightarrow {AB}\) на ось можно считать отрезок \(\displaystyle A'B'\), взятый со знаком <<+>>.

Рассмотрим ситуацию, когда брусок движется по наклонной плоскости:

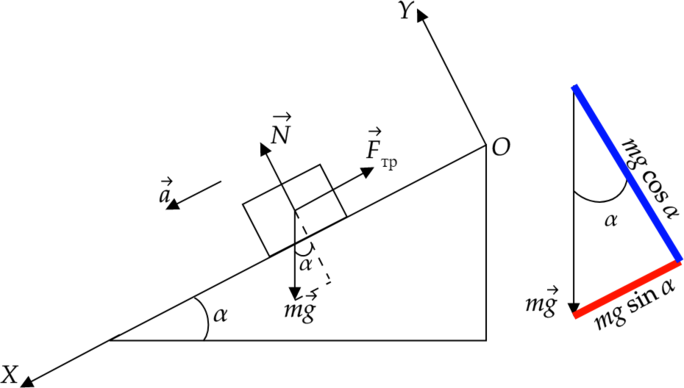
Исходя из рисунка мы можем записать II закон Ньютона в векторной форме: \[\vec{F}_\text{тр}+m\vec{g}+\vec{N}=m\vec{a}\]

Запишем теперь проекции на оси:

\[OY:-mg\cos\alpha+N=0\] \[OX:-F_\text{тр}+mg\sin\alpha=ma\]

Посмотрим, как получили два вышеприведенных равенства. Направим оси, как на рисунке, тогда по оси \(OY\) ускорение и сила трения на тело не действуют, так как они направлены перпендикулярно этой оси, а проекции сил, перпендикулярных оси, равны нулю.

Сила реакции опоры направлена по оси \(OY\), значит, возьмем ее положительную проекцию.

Также рассмотрим силу тяжести, вектор которой НЕ КОЛЛИНЕАРЕН осям координат, разложим его на два составляющие (см. рисунок сбоку) и возьмем синюю линию, являющуюся проекцией силы тяжести на ось \(OY\). Из простых геометрических соображений видим, что она равна \(-mg\cos\alpha\).

Аналогично действуем для оси \(OX\).

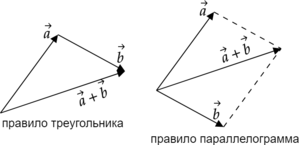
Сложение векторов можно производить по правилу треугольника или по правилу параллелограмма, рассмотрим на примере.

Даны векторы \(\vec{a}\) и \(\vec{b}\), по правилу треугольника мы можем получить сумму \(\vec{a}+\vec{b}\), совместив конец вектора \(\vec{a}\) с началом вектора \(\vec{b}\).

Даны векторы \(\vec{a}\) и \(\vec{b}\), по правилу параллелограмма мы можем получить сумму \(\vec{a}+\vec{b}\), совместив начало вектора \(\vec{a}\) с началом вектора \(\vec{b}\).

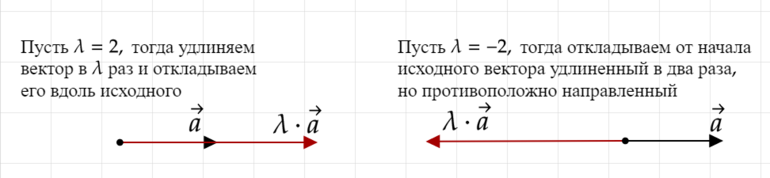
Умножение вектора на число.

Рассмотрим различные варианты произведения вектора \(\vec{a}\) на какое-то вещественное число \(\lambda\):

1) \(\lambda=0\)

\[\vec{a}\cdot0=\vec{0}\]

При умножении на нулевое число получается нулевой вектор (вектор нулевой длины);

2) \(\lambda>0\)

При умножении на положительное число получается вектор, сонапаравленный исходному вектору (происходит просто “удлинение” или “укорачивание” нашего вектора, направление не меняется);

3) \(\lambda<0\)

При умножении на отрицательное число получается вектор, противоположно направленный исходному вектору (происходит “разворот”  вектора на 180 градусов и изменение его длины одновременно).

Скалярное произведение

Скалярным произведением векторов называют число, равное произведению длин этих векторов на косинус угла между ними.

Обозначение скалярного произведения векторов \(\vec{a}\) и \(\vec{b}\) имеет вид \((\vec{a},\vec{b})=|\vec{a}|\cdot|\vec{b}|\cdot\cos\Big(\widehat{\vec{a},\vec{b}}\Big)\)

Физический смысл скалярного произведения

Работу \(A\) тела, перемещаемого из точки \(M\) в \(N\) с постоянной силой \(\vec{F}\), можно найти как произведение длин векторов \(\vec{F}\) и \(\overrightarrow{MN}\) с косинусом угла между ними, значит работа равна скалярному произведению векторов силы и перемещения:

\[A=\Big(\vec{F},\overrightarrow{MN}\Big)\]